一，推荐方法

下单渠道1位+支付渠道1位+业务类型1位+时间信息4位+下单时间的Unix时间戳后8位（加上随机码随机后的数字）+用户user id后4位。然后你会说，这样算下来就订单号就19位了啊，一点都不精简啊，不好记不好念不好输的。但我说的上面的这些业务标记，你不一定要全部加上啊。

你看淘宝/天猫那么大的订单量，16位订单号就搞定了。细心的网友已经发现了，订单号的后4位是取自用户user id的后四位，前12位中有10位可能是由Unix时间戳加随机规则生成的。

二，从用户体验和数据库优化的角度来看

1.利用数据库主键值产生一个自增长的订单号（订单号即数据表的主键）

2.日期+自增长数字的订单号（比如：2012040110235662）

3.产生随机的订单号(65865325365966)

4.字母+数字字符串式，字母有包含特别意义，C02356652

5.订单号无重复性；

6.如果方便客服的话，最好是“日期+自增数”样式的订单号，客服一看便知道订单是否在退货保障期限内容；

7.订单号长度尽量保持短（10位以内），方便用户，尤其电话投诉时，长的号码报错几率高，影响客服效率；

8.订单号尽量保持数字型(纯整数)，在数据库订单索引查询中，长整数字型的数据索引与检索效率，远远高于文本型，因此尽量避免“字母+数字字符串式”！

三，首先，订单号不适合用自增字段，因为会暴露一个网站的业务量。另外，通常在订单在写入数据库之前，业务就需要用到订单号了。网上多数用microtime生成的时间戳生成唯一订单序列号，事实上高并发情况下有一定的重复几率，就连uniqid（$more_entropy参数为false）函数生成的序列号都可能有重复的可能（真坑爹），而$more_entropy设置为true的话返回的序列号又太长了。

不依赖外部流水号，完全靠时间戳和随机数生成订单号无法避免冲突，所以必须引入外部的流水号生成机制。或使用数据库，或使用APC之类的缓存。用APC之类的缓存存在一个问题，就是无法持久保持数据，服务器重启或者PHP宿主进程重启都会清空流水号计数器，所以可以采取缓存+数据库结合的模式——如果缓存中有流水号计数器数据则读取并累加计数，如果缓存中没有流水号计数器从数据库中还原计数器。计数器可以每隔一段时间重置一次。

既然引入了自增流水号计数器，又会导致文章开头的“德国坦克问题”，所以需要用skip32算法把流水号加密（https://github.com/nlenepveu/Skip32）。

补充：

什么是“德国坦克问题”，

那时候，德国制造的每一辆坦克上都有一个序列号。假设德国每个月生产一批坦克，从1到最大值N顺序排列，因此，可以把这个最大编号N，当作每个月总的生产量。盟军发现和截获的任何德国坦克上的序列号，都应该是介于1和N之间的一个整数，根据这些截获坦克序列号的数据，如何来猜测总的生产数N？这是当年的战争给数学家们提出的难题。

这是一个统计推断的问题，也就是从观察到的数据样本（序列号），来推断随机变量的某些整体参数（N）。如今思考这个问题，有两种不同的推断方法：经典方法和贝叶斯推断。

经典方法

经典统计推断包括几个基本原则：最大似然（概率）估计、最小方差、无偏性等等。简单而言，经典统计使用求极值的方法，让选取的某个似然函数最大化，同时也考虑样本平均平方差最小化，而无偏性指的则是尽量使得样本平均值等于整体平均值。

比如说，先考虑最简单的情况：在某个月内，盟军只发现了1辆德国坦克，其标号为60，那么，你如何来估计德国在这个月生产坦克的总数N？也许读者会说：“你疯了！只有这么1个数据，有什么可估计的？还能使用什么统计方法吗？参数N是任何数值都有可能的，只能随便猜测一个啦！”

不过，你的说法显然不正确。首先，N不可能是任何数，N的值起码要大于或等于60！严肃的统计学家就更不会这么说了，即使对如此少量的数据，他仍然可以进行他的统计推断。

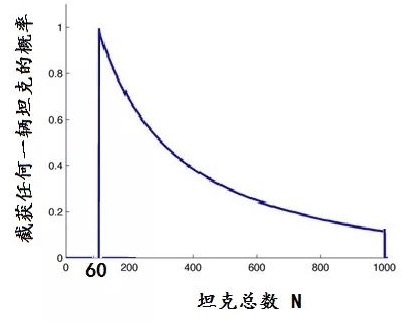
第一，为了估计真实的总产量数N0，他需要构造一个概率函数，称其为似然函数。设想：如果这批坦克生产的总数是N的话，根据等概率原则，拦截到1到N中任何一个编号的坦克的可能性都相同，均为1/N。也就是说，截获任一辆坦克的概率是坦克总数N的函数：N越大，即生产的坦克数越多，截获某个编号坦克的概率便越小。概率随N的变化情形，如图3所示的一截双曲线。这个概率分布曲线，便可选作似然函数。

最大似然估计的目标是找出概率最大的点对应的N0，因为这个问题中，N越小概率越大，所以得到在最大化概率点的N0=60，即图3中曲线最左边的起始点。

经典方法的第二个考虑是最小化均方差（MSE）。为此，我们假设总产量N不是刚好等于60，而是乘以一个大于1的因子a。想象盟军看到了N个坦克中所有的坦克，那么，均方差可以按照如下方法计算并最优化，再求最小值。

从上面的计算结果，当坦克总数N比较大时，相乘的因子a近似为3/2，由此可将N0的估计值从60，调节到N0 (均方差最小) = 60×3/2 = 90。

最后，还得考虑样本的无偏性。如果N0=60的话，这个样本太不符合“无偏”的条件了，既然每一辆坦克被发现的概率都是一样的，凭什么盟军截获了一辆坦克就截到了最后生产的那一辆呢？这听起来太奇怪了，N0=90也不符合无偏，最符合无偏条件的就是截获的是序号为中间的那一辆，它的序号使得样本序号的平均值等于整体所有样本序号的平均值。也就是说，无偏的N0被估计为60的两倍，N0 (无偏)=120.

真不愧为数学家，仅仅截获到1辆坦克，就有这么多的考虑，如果截获了更多呢？我们可以将问题一般化，以上经典学派的思考方式也可以推广到一般的情况，简单叙述如下：

问题：盟军发现了k辆坦克，序号分别为i1……ik，最大的序号是m，估计总数N0。

经典推断方法的答案：N0 = m + (m-k)/k。

比如说，盟军发现了5辆坦克，其序列号分别为215、90、256、248、60，因此，k = 5，m = 256。从以上经典方法的公式，得到坦克未知的总数N0 = 256 +（256-5）/5 = 306。

贝叶斯派的推断过程

假设盟军截获的第一辆坦克序列号是215，从前面频率派方法最开始的一段分析可知，对应这1个样本，N可能是从215开始的任何整数，但是，N值越大，概率越小，我们暂时忽略N值大于1000的情况，可以画出N的概率分布是类似于图3的双曲线，不同的是曲线的起始点和形状，图3中的曲线参数N0=60，这儿的参数N0=215，见图5a中最大值在N0=215处的“序列号215分布”曲线（蓝色）。

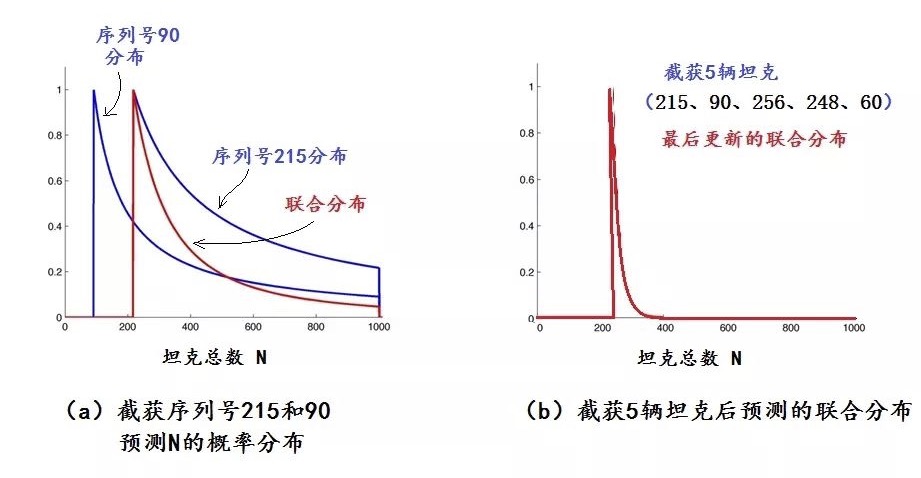
现在，我们加上第二辆坦克的信息：序列号90。因为90小于215，它的出现并不改变似然函数的最大值，但是它却对N的分布曲线有所影响，两个变量的联合分布曲线用图5a中的红线表示，这也是加上第二个数据之后更新了的参数分布。如图可见，序列号90的数据使得概率分布曲线变得更尖锐，说明N的较大数值出现的概率大大降低。

如果再加上后面3个样本：序列号256、248、60，五个样本的联合分布变得更为尖锐，峰值是256，N=400到1000的概率已经几乎为0，可以忽略不计了，如图5b所示。

在这个具体例子中，最后对N0的估计：频率派的N0 = 306，与贝叶斯派的N0 = 256相差不大，难分孰优孰劣。然而，通过该问题，我们简单了解了频率派和贝叶斯派的不同思考方法。

不少学者认为贝叶斯分析的方式和人脑的工作机制有相似之处，这也是为什么近年来将贝叶斯统计方法广泛应用于人工智能研究，特别是机器学习领域的原因之一。当今人工智能技术的崛起，部分归功于计算和统计的联姻，实际上也就是说，归功于计算机和贝叶斯方法的联姻。

来源：

https://www.jianshu.com/p/544ab3d60e77

https://www.zhihu.com/question/19805896/answer/131710504

https://www.jianshu.com/p/8ce87ffc1732

https://blog.csdn.net/vucndnrzk8iwx/article/details/79550808